生体信号解析

生体信号に対する新しい非線形解析法の紹介

　医学分野では生体現象を解釈するため生体信号を表示・記録し解析する．生体信号をモニターすると臨床現場では表現することが多い．生体信号は心電図，脳波，呼吸運動，胃電図など非常に多くの装置が実用化されている．これらは生体から出力された1変数の振幅を縦軸にして，横軸は時間をパラメーターにして展開した表示法が主に使用される．表示されている信号は本来生体がもっている高次元情報からの射影，すなわち影と仮定できる．1変数の生体信号から元となったシステムを推定することを目的とする．

　生体現象の多くは非線形的変動を認める．呼吸生理の分野でも新しい種類の非線形解析法の応用報告がなされている．“埋め込み定理”を用いて再構成した高次元座標空間に時系列データを物体（アトラクタ）として埋め込み,アトラクタの特徴を解析する方法が利用される．周期解析などの線形解析と違い，本法は新しい観点から解析できる．

呼吸運動は線形解析により明らかな主周期が認められる．最近になり従来ばらつきと考えられていた“ゆらぎ”を考慮すると非線形的現象であると明らかにされた．非線形解析法のうち，“埋め込み定理”を利用して高次元空間に物体（アトラクタ）として埋め込み，複雑系を記述する指標としてアトラクタの特徴を解析する方法が用いられている．他方，フーリエ変換から求めた線形記述では解析した過去の時系列データのみは再現できるが，近い未来すら予想はできない．従って予測性，複雑性などを加味した方法として新しい種類の非線形解析法は有用である．

時系列データのアトラクタ次元はGrassberger-Procaccia法により相関次元(D2; correlation dimension)として求められる．相関次元は数学者Alfred Renyiの情報理論から派生したものであるが広義のフラクタル次元の一種として説明されることがある．相関次元をD2と略すのは，一般化次元 Dq の q=2 の場合から導き出されたためである．得られた結果は非線形性を検定するためsurrogate dataから得られた結果との比較が必ず必要である．適用時の注意点を概説する.

生体信号に対する新しい非線形解析法の概略

 
＃１　生体現象の時系列データを記録する．
＃２　アナログデータの場合，A/Dコンバーターで等間隔にサンプリング．
＃３　埋め込み定理による時間ずらしでベクトル再構成．
＃４　再構成座標空間（時間遅れ座標空間，状態空間）に埋め込み．
＃５　相関積分を計算（各ベクトル周辺の他ベクトルの存在確率）
＃６　相関次元，approximate entropyなどを計算

　自己流に解釈にすると，生体現象の１変数，時系列データから再構成したベクトルを高次元空間に埋め込み図形（物体）として表し，背景に存在する決まりごとを推測する方法である．図形の性質を相関積分を用いて再構成したベクトル周辺の確率として変換し，複雑性，予測性を統計量として解析する．埋め込んだ物体は3次元空間までは簡単に図示できるので直感的に感じることもできる．
　物体を埋め込む次元は何次元でも可能である．高次元で呼吸運動の軌跡を考える利点として，例えば2次元では軌跡は重なり合って特徴がみえない．3次元だと立体的に見える．しかし，3次元でも重なり合って絡み合っている可能性もあるため，高次元で絡み合っていない状態で検討できたらよい．新しい種類の非線形解析は特徴を何次元の立場でも検討・解析できる．



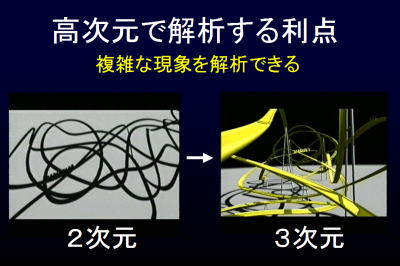
1変数の時系列データから，アトラクタを再構成して高次元情報を推測可能である．
逆に，３次元空間で測定された現象をいったん１次元のデータに落として，任意の高次元空間にアトラクタを再構成し，その高次元空間にジャンプさせ解析することもできる．

現象を規定する数式を明らかにする必要がなく，数式で記述できない複雑な現象も簡単に解析できる．特に予測性，規則正しさ，複雑性を明らかにしたり，背景に全く決定論がないこともある程度証明できる．

　埋め込んだ物体は3次元空間までは何らかの方法により針金のようなもので自動的に作製できれば，さわることも可能である．意味ある決まりごとかどうかは客観的な検定が必要である．その検定法の１つが，surrogate data analysis である．Surrogate data analysis は完全ではないため今後さらなる検討は必要である．
.

３次元（埋め込み次元３）の空間に時系列データを
埋め込む概念図 （ｍ＝３）
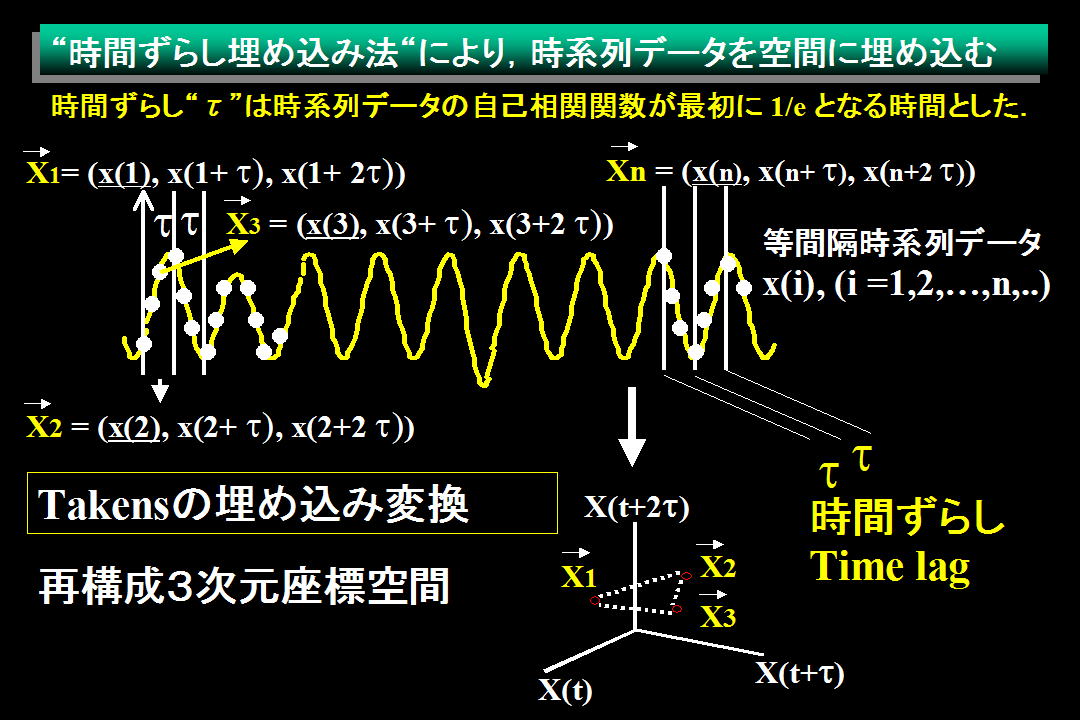
等間隔の時系列データを　x(i)　(i = 1 〜 N) とすると，高次元空間に埋め込むため，時間ずらし埋め込み法で新しく再構成したベクトルは以下の如くになる．

 

Grassberger-Procaccia 法

　Grassberger-Procaccia法は１変数の時系列データを埋め込み定理で高次元空間中に再構成し，アトラクタの特徴をあらわす相関次元を求めるための方法である．各データ間が等間隔の時系列データ[x(1), x(2), x(3),…, x(N),…]から，ポイント数Nのデータをm次元空間に埋め込み定理を用いてプロットするために，時間ずらしで再構成した各データセットをベクトルXiで表す．

Xi = {x(i), x(i + τ), ･･･, x(i + (m - 1)τ)}, (i = 1 〜 N)

基準となる点Xi を選び，残りの（N-1）個の点に対してXi から各々の点までの距離 |Xi-Xj| (j = 1 〜 N)を計算する．そして，基準とした点Xi からある一定の距離 r 内にあるデータの点を数え，すべての i に対してこの処理を繰り返して，次式のような相関積分と呼ばれる統計量を得る．距離 r は変数である．

                                 　N   N  
              Cm(r) =1/N² ΣΣ Q(r-|Xi-Xj|)             
                           　　　i=1  j=1

ただし，Q(t)はヘビサイド関数で，If t ≧ 0, Q(t) = 1；If t < 0, Q(t) = 0である． m は埋め込み次元（embedding dimension）を意味する．この相関積分に次式　（Mandelbrotのフラクタルの定義式）のような比例関係があるとき，埋め込み次元m（空間の軸の数）のアトラクタの相関指数は s であるという．

                            Cm(r) ∝ r^s

さらに，両辺の対数をとり，次のような比例関係が得られる．

                            log Cm(r) ∝ s log r

相関積分の解釈：１変数の時系列データを時間ずらし埋め込み法（埋め込み定理）で再構成した各データセットとしてベクトルに変換し，距離 ｒ で特定の点（ベクトル）周囲の他点の存在分布確率を計算することになる（下図参照）．この操作をすべてのベクトルに対して行う．

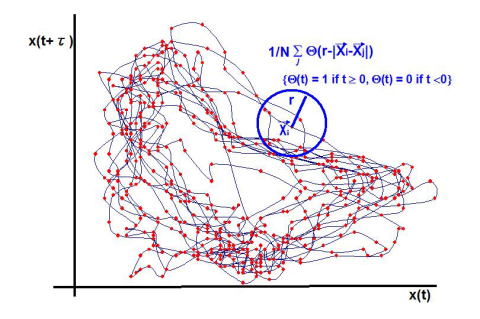
　カオスモデルなどのノイズのない時系列データにおいて相関積分曲線は直線になるため，相関指数 s はどの r においても同一の値を理論上得ることができる．しかし，ノイズの多い実験データの場合，直線となる部分が限られているため相関指数 s は適当な距離 r の範囲(scaling region)における log r に対するlog Cm(r)の傾きで与えられる．次いで，再構成座標空間への埋め込み次元mに対する相関指数 s のグラフを描き，埋め込み次元 mが大きくなるにつれ s が飽和したところの値を真のアトラクタの相関次元D2とする．飽和を認めないならば，少なくとも決定論的特徴はない．

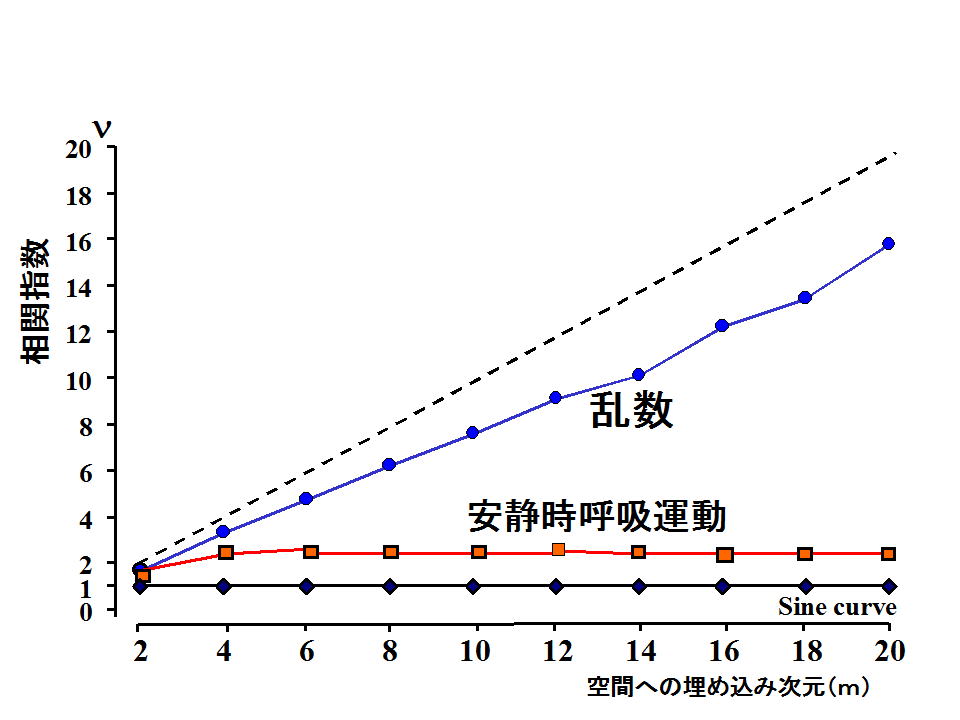
　睡眠中，stage IVの呼吸運動の解析例を示す．具体的には図１のように相関積分曲線（図１A）から局所の傾きに相当する相関指数を計算し，変数の距離log r−相関指数 s のグラフ上(図１B)プラトーの部分が存在するか確認する．プラトーの部分が存在しなければScaling regionの設定はできない．プラトーの部分が存在すれば一定の間隔でScaling region を決める（図１）．Scaling region は大きいほど妥当性がある．次に各埋め込み次元ごとに，その Scaling region 間の相関指数を最小二乗法かTheilerの”rule of five” (Theiler J and Lookman T. Statistical error in a chord estimator of correlation dimension: The "rule of 5". Int J Bifurcation and Chaos 1993; 3: 765-771.) で決定し，図２のような横軸が埋め込み次元，縦軸が相関指数の図を作成する．図２のシミュレーションのようにサインカーブやトーラスの如き明確な相関指数の飽和状態（プラトー）が存在すれば，水平線を引き縦軸と交わる値を相関次元とする．単純に相関指数が相関次元そのものではないことに注意すべきである．

　実験データの場合，Grassberger-Procaccia法はfalse positiveが多いため元データ（original data）からsurrogate dataを作成し同じ計算過程を行った結果との比較が必ず必要である．surrogate dataとはoriginal dataに非線形的特徴があるかどうかを検定するさいに用いられるもので(null hypotheses)，original dataから作られ，original dataと同じ平均，分散，周波数分布，自己相関関数をもち，さらに乱数である，線形性を有するという特徴をもたせ，非線形的な特徴を有さない時系列データである．

 

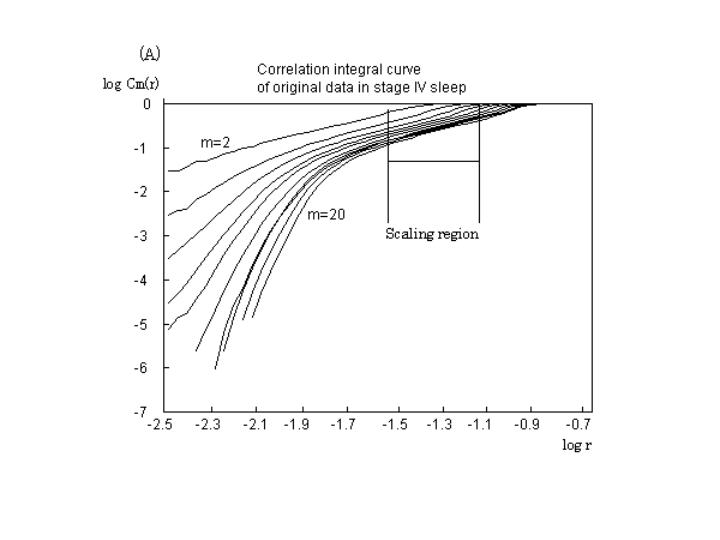
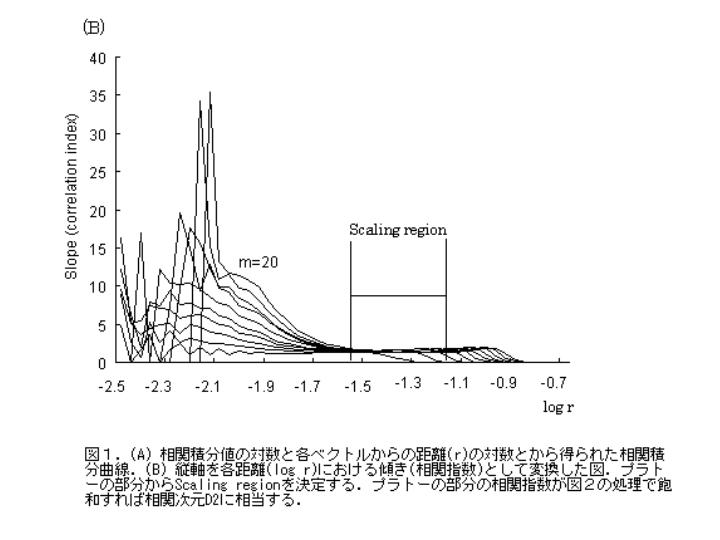
(A)で距離 r が大きい部分は直線となっている。しかし、小さい部分は大きく曲がり曲線となっている。特に埋め込み次元 m が大きくなると曲がりが大きい。

　解釈として比較的巨視的（各ベクトルの存在確率を大きな r で求めると）に考えると、いわゆる少数自由度のカオスに近い挙動をしめすが、カオスモデルと根本的に異なるのは、小さい視点（各ベクトル近傍）で考えると（各ベクトルの存在確率を小さな r で求めると）まったく背景に決定論的根拠がないことを意味する。

　生体信号のノイズのためなのか、小さい視点では少数自由度の挙動の如く見えていた各サブシステムの多数の要素が見えてきたのか、これだけの結果では明確ではない。言えることは、数学的カオスモデルのノイズのない時系列データにおいて相関積分曲線は直線になるため，相関指数 s はどの r においても同一の値を理論上得ることができる．したがって、本来の定義式にある r → 0 により相関次元が求められる。一方、実験データは scaling regionという幅を持って求めなければならない。

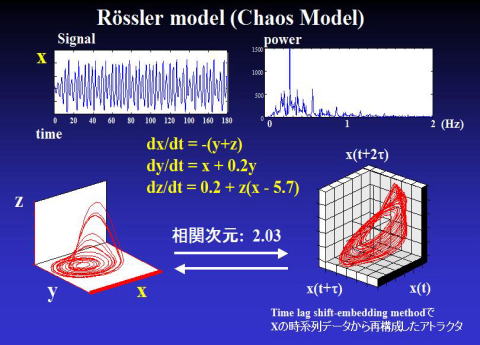
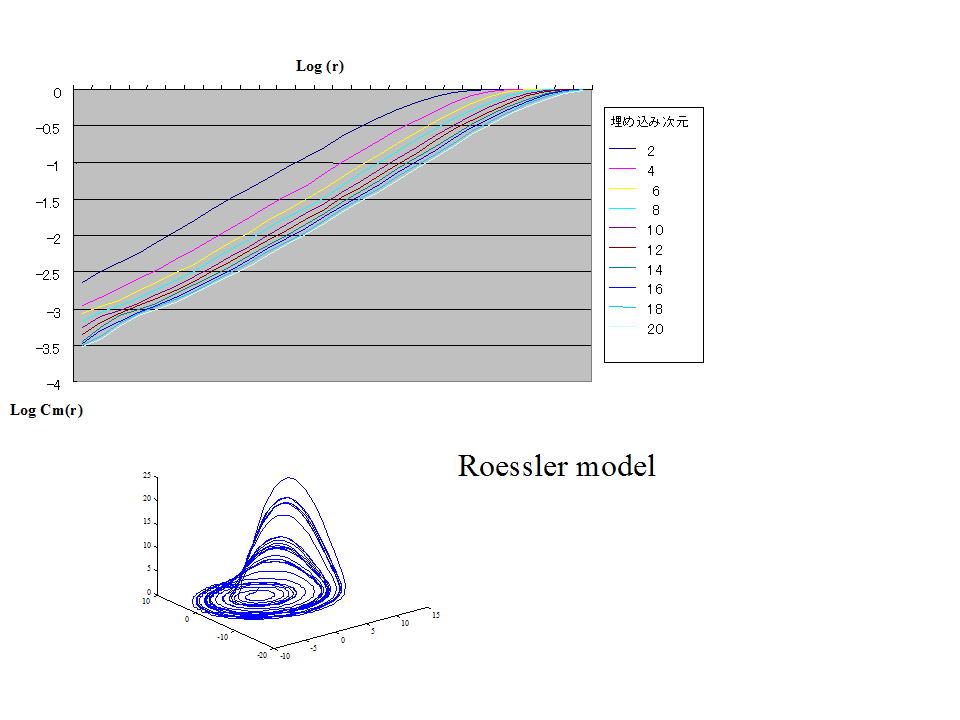
実際，代表的なカオスモデルのレスラーモデルの，log (r) vs. log Cm(r)の関係は下図のように，直線となっており，本来の定義式にある r → 0 により相関次元が求められる。これはカオスモデルのレスラーモデルは直線の傾きが理論上，どこでも同じためである．

log (r) vs. log Cm(r)の直線の傾きは　約2.03 程度である．したがってレスラーモデルのアトラクタの相関次元は　2.03 となる．

相関指数飽和の解釈：

図２は時間ずらし埋め込み法を用いて再構成した軌跡，アトラクタの相関指数を空間の軸数に相当する埋め込み次元（ｍ）ごとに Grassberger-Procaccia法を用いて計算した結果．
サインカーブは相関次元１，トーラスは２，呼吸運動は２より少し大きい値で飽和している．
乱数は飽和しない．飽和しないことから乱数の背景には決定論的なものがないことを示唆する．
ここで注意すべきは非整数次元が求まったからといってカオスと考えてはいけない点である．

埋め込み次元を増加させ相関指数が一定の値を示すことを確認する意味として以下の解釈があると思われる．
埋め込み次元 m は状態空間（再構成座標空間）の軸数である．例えば”ボール”を 0次元でみたとき”点”となる．1次元でみたとき”線”，2次元では”閉曲線”である．3次元以上ではじめて”ボール”の特徴となる．アトラクタも同様に一定の埋め込み次元以上で，相関指数が飽和し，アトラクタの特徴をあらわす指標のひとつである”相関次元”が決定できる場合のみに一定の特徴があり，背景に何らかの決定論がある可能性が推測される．乱数から再構成されたアトラクタの相関指数は図２のように飽和しないため一定の特徴をもたないことがわかる．従って，再構成座標空間の軸数と同じ値の埋め込み次元を増加させて相関指数の飽和を確認する操作は，アトラクタの元となった時系列データの特徴を解析するために必須である．

呼吸運動の複雑系

　Grassberger-Procaccia法を用いて呼吸運動の相関次元が求まる．近年，生体信号とカオスの関連が議論されている．相関次元が求まってもカオスであると断定できない．この点で従来の多くの報告に問題がある．生体現象は多数の要因が関与するが，いくつかの要因がサブシステムを作って見かけ上，小数自由度の挙動を示している可能性もある．
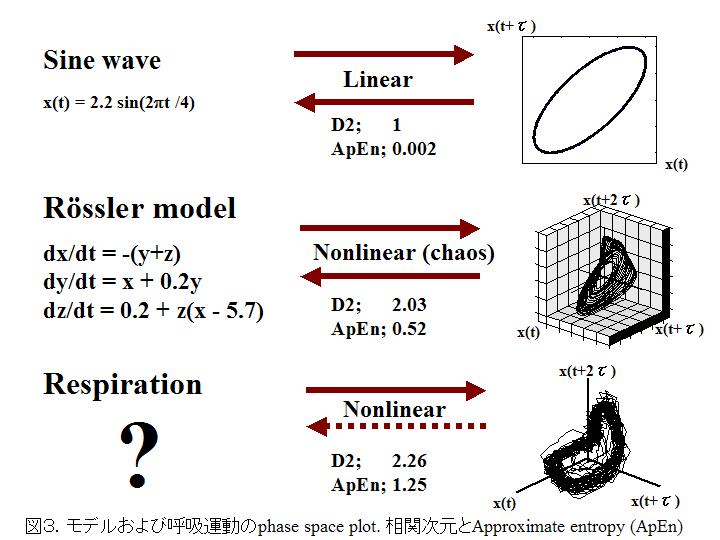
　さらにGrassberger-Procaccia法から，図3に示したように元となるモデルを推定することはできない．カオスは非常に特殊な状態であるため，真に生体現象がカオスのみで説明できるか否か，いまだ検討を要する．最近になり複雑系の観点から現象の予測可能性を検討するためPincusが報告したapproximate entropy (近似エントロピーApEn)が生体信号の解析に用いられている．正弦波のような規則正しい運動で予測可能性が高い信号の値は０になる．乱雑さが増せば値は大きくなる．図3のようにApEnはカオスモデルのRossler modelより呼吸運動でかなり大きい値をとる．呼吸運動は数学的なカオス以外の非線形的法則が背景にあると思われる．
　カオスは予測不能とよく表現される．これは初期値に対して敏感であることが大きな特徴であり，レスラーモデルは式で表される点に注目すべきである．一方，呼吸運動はアトラクタとしての特徴の一部を数値化することは可能であるが，一般的な式で表すことは困難である．数学的概念と生体の生理学的変化をカオスとして同一視するのは直感的に間違っている．

近似エントロピー（ApEn）に関しては（文献7，9，10）を参照してください．
簡単には以下のようになる．

Approximate entropy ＝ Φ_m(r) −Φ_m+1(r)

                      　    N-(m-1)
Φ_m(r)=[N-(m-1)]^-1Σ log_eCm,i (r)      
                           　 i=1

                        　     N-(m-1)
Cm,i (r)=[N-(m-1)]^-1Σ Q(r-|Xi-Xj|)     
                                 j=1

対数を利用している点でエントロピーの一種となる．
下限は周期運動で０である．利点は値に上限があり，実験データで統計処理を行いやすい．上限は時系列データ数によって異なる．
また本式は Korgomorov-Sinai entropyの定義式を若干変形すると得られる．
近似している点で "approximate"と Pincus は論文中で呼称したと思われる．

問題点と今後の展望

呼吸運動は，単なる周期運動にノイズが加わっただけではなく何らかの決定論的現象の存在する可能性は高いと考えられる．しかし，実験データにこれらの非線形解析を適応するには十分な注意が必要である．

１．時系列データは補間データを用いるべきではない．

従来の報告の中には不等間隔の時系列データを補間処理して等間隔データに変換した上で埋め込み定理を用いてアトラクタを再構成し，相関次元あるいはリアプノフ指数を計算した報告が多かった．補間処理そのもので複雑系システムのもとになる非線形的特徴の多くが消失するため，補間データから得られた結果の妥当性はない．すなわち，循環器領域でよく用いられているRR間隔の解析は補間処理のみで非線形的特徴の多くは消失する．従って補間処理した心拍変動から得られた相関次元は妥当性が少ないと思われる．

2. Grassberger-Procaccia法を厳密に適応すべきである．

本稿に相関次元を実験データからGrassberger-Procaccia法で求める手順を簡潔に記載した．特に埋め込み次元を増加させ相関指数が飽和するか否かは必ず確認が必要である（図２）．したがって，相関指数の飽和を確認していない特定の埋め込み次元の相関指数を相関次元とすることはノイズが多く含まれアトラクタ局所での周辺ベクトルの存在確率がばらつく実験データでは全く意味をなさない．我々の検討では，通常状態の脳波は飽和しないことが多く，これまでの多くの報告に疑義が残る．しかし，てんかん発作時の脳波は飽和する場合が多かった．

3． surrogate dataとの比較が必ず必要である．

Grassberger-Procaccia法はfalse positiveが多い．Original dataから計算された相関次元は,，非線形性を検定するためsurrogate dataから得られた結果との比較が必ず必要である．Surrogate dataとの比較がない結果から相関次元の有意性を議論できない．通常，39個のsurrogate dataから各々相関次元を計算し，Z変換を行い検定する．Surrogate dataは線形ランダムなので平均した値はoriginal dataから計算された相関次元より大きくなる．有意の差がなければoriginal dataは線形ランダムな性質しか持たない可能性が高い．
　他の指標（リアプノフ指数など）でもsurrogate dataから得られた結果との比較が必要である．我々の検討でヒトから得た実験データから意味のある有意なリアプノフ指数を得ることは困難であった．この点でも少数データからリアプノフ指数を計算した従来報告に対して疑問がある．

生体現象が非線形的特徴をもち，何らかの法則が背景にあるのは間違いないと推測される．われわれの解析から，本質は決定論的カオスのみにある可能性は低く，今後も検討が必要である．カオスにとらわれず線形現象，非線形現象，ノイズなどの信号にすべて適応できるエントロピーの検討が新しい局面を開くかもしれない（文献7，9，10）．

４. Grassberger-Procaccia法から求めた生体信号データの相関次元は定義された相関次元と同じ統計量か？

上記に記載した実験データから求めた相関次元は数学者Alfred Renyiの情報理論から派生した一般化次元の q=２の情報統計量と同じか疑問である．
実際，生体信号データからlog (r) vs. log Cm(r)の直線の傾きは変数 r が大きいところでは直線となっているが，小さいところでは大きく曲がっており，相関指数が埋め込み次元の増加で飽和しない．
従って，生体信号データから計算された相関次元は制限がついていると思われる．
リアプノフ指数を生体信号データから求めるのは，log (r) vs. log Cm(r)の直線の傾きは変数 r が大きいところでは直線となっているが，小さいところでは大きく曲がっており当然無理と思われる．
言い換えると，相関積分を計算時に使用する超球の半径 r が大きいとき（巨視的に考えたとき）相空間における軌跡がつくるアトラクタの性質は同じ（相関指数は埋め込み次元増加でも同一）にみえるが，超球の半径 r が小さいとき（近傍で考えたとき）アトラクタの性質は規定されない（相関指数は埋め込み次元増加で発散）．

文献

1. Takens F. Detecting strange attractors in turbulence. In: Lecture Notes in Mathematics (Rand DA and Young LS, eds), 1981, Vol. 898. pp 366-81. Berlin: Springer-Verlag.
2. Kaplan DT. Geometrical techniques for analyzing ECG dynamics. J Electrocardiography 24(Supl): 77-81, 1992.
3. Grassberger P, Procaccia I. Characterization of strange attractors. Phys Rev Lett  50: 346-9, 1983.
4. Grassberger P. Dimensions and entropies of strange attractors from a fluctuating dynamics approach. Physica D  13: 34-54, 1984.
5. Theiler J, et al. Testing for nonlinearity in time series: the method of surrogate data. Physica D  58: 77-94, 1992.
6. Burioka N, Cornelissen G, Halberg F, Kaplan DT. Relationship between correlation dimension and indices of linear analysis in both respiratory movement and electroencephalogram. Clin Neurophysiol 112(7):1147-1153,2001.
7. Burioka N, Cornelissen G, Halberg F, Kaplan DT, Suyama H, Sako T, Shimizu E. Approximate entropy of human respiratory movement during eye-closed waking and different sleep stages. Chest 123:80?86, 2003
8. Miyata M, Burioka N, Sako T, Suyama T, FukuokaY, Tomita K, Higami S, Shimizu E. A short daytime test using correlation dimension for respiratory movement in OSAHS. Eur Respir J 23:885-890,2004
9. Burioka N, Miyata M, Cornelissen G, Halberg F, Takeshima T, Kaplan DT, Suyama H, Endo M, Maegaki Y, Nomura T, Tomita Y, Nakashima K, Shimizu E. Approximate entropy in electroencephalogram during wake and sleep. Clin EEG Neurosci. 36(1):21-4, 2005.
10. Burioka N, Cornelissen G, Maegaki Y, Halberg F, Kaplan DT, Miyata M, Fukuoka Y, Endo M, Suyama H, Tomita Y, Shimizu E. Approximate entropy of electroencephalogram in healthy wake and absence epilepsy. Clin EEG Neurosci. 36(3):188-93, 2005.
11. Burioka N, Cornelissen G, Otsuka K, Shimizu E, Halberg F. Linear and nonlinear indices of variability in respiratory movement, the electroencephalogram and the electrocardiogram. Neuroendocrinol Lett 24 (supple 1): 223-230, 2003.